齊藤 宣一
偏微分方程式の数値解析
田端 正久 著
岩波書店, 2010年
本書は，偏微分方程式の代表的な数値的解法である，差分法，有限要素法，境界要素法に対する数学的な理論の，基礎の導入から，収束証明にいたるまでを，丁寧かつ明快に解説した，数値解析の入門書である．コンピュータに関わる諸技術の発達に支えられ，コンピュータ・シミュレーションは，理工学に留まらず，経済学や生命科学にまで応用範囲を拡げ，現代の科学技術における主要な解析方法の一つになっている．その中の一つの柱として，様々な数理モデル，すなわち偏微分方程式を数値的に解くという作業がある．したがって，偏微分方程式の数値解法の解説には，数学者の立場から見て違和感がなく，応用家の立場から見て実用性があることの二面性が要求される．この要請を満たしている洋書の多さに比較して，和書の数は心もとなく，かろうじて菊地文雄先生の著作が思い浮かぶのみであった．そこに，ようやくもう一冊として，本書が加わったというのが，評者の正直な感想である．実は，本書は，1994年に岩波講座「応用数学」の一分冊として刊行された「微分方程式の数値解法II」に，新たな章を加えて，改めて単行本として出版されたものである．長い間，分冊の方を手に入れにくい状況が続いていたので，本書が，再び多くの人の手に届くようになったことは喜ばしい．そして，著者の田端正久先生は，この分野の国際的な指導者の一人であり，その田端先生による著書を，日本語で読める日本の読者は幸せであると思う．
本書の内容を概観すると次のようになる．第1章は，差分法である．空間2変数のPoisson方程式を題材に，差分法を導入して，その後，熱方程式を題材に，安定性に関するvon Neumann条件が解説されている．そして，一般の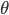 
スキームに対する安定性，適合性と収束性や，最大値原理が説明されている．
第2章は，有限要素法の解説である．有限要素法の数学理論を論ずる場合，Sobolev空間等の関数解析の言葉がどうしても必要となる．第2章（と第4章）のはじめには，必要となる関数解析の必要事項が証明抜きで説明されている．本書や他の数値解析の洋書を読む際にも便利であろうし，本書を先に読んで，動機付けを行った上で，関数解析の学習に進むことも有意義であると思う．勉強の順番は一意的ではないのである．それはともかく，本章では，有限要素法の数学的基礎事項が，短い頁の中でほぼ説明され尽くしている．とくに，有限要素関数の補間誤差評価が，一般の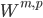 
ノルムに対して証明されており，現役の研究者にも，大変貴重である．その他にも，集中質量近似や，時間発展方程式の解説もあり，この分野の洋書と比べても，内容自体は豊富である．
第3章は，境界要素法の解説であるが，これも，計算の現場ではポピュラーな方法であるにも関わらず，いままで数学的に信頼のおける解説はあまりなかったため，今後，重宝されるはずである．
さて，本書の一つの目玉は，新しく追加された第4章であり，混合型有限要素近似の解説である．流体力学の基礎方程式であるNavier-Stokes方程式の有限要素近似の際に本質的な役割を果たす，いわゆる下限上限(inf-sup)条件の解説は，他のどの本・論文よりも，その本質を捉えたものであり，この部分を読むだけでも，本書を手に取る価値があると思う．
なお，本文の中に，具体的な数値計算方法の説明や数値計算例は，ほとんど述べられていないが，それはむしろ，読者の自習に委ねられていると考えるべきであろう．
評者は，本書の前身となった分冊を学生時代に勉強し，研究者としての基礎素養を身につけた．それから，20年近い時を経て，改めて出版された本書が，再び多くの人達に影響を与え，多くの若い人材が数値解析の分野に参入してくることを期待したい．
さいとう のりかず
東京大学大学院数理科学研究科
[Article: J1207A]
(Published Date: 2012/12/18)